Point at infinity
The point at infinity, also called ideal point, of the real number line is a point which, when added to the number line yields a closed curve called the real projective line,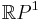 
. The real projective line is not equivalent to the extended real number line, which has two different points at infinity.
The point at infinity can also be added to the complex plane,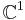 
, thereby turning it into a closed surface (i.e., complex algebraic curve) known as the complex projective line, 
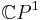, also called the Riemann sphere.
In an affine or Euclidean space of higher dimension, the points at infinity are the points which are added to the space to get the projective completion. The set of the points at infinity is called, depending on the dimension of the space, the line at infinity, the plane at infinity or the hyperplane at infinity.
Contents |
Projective plane
Consider a pair of parallel lines in an affine plane A. Since the lines are parallel, they do not intersect in A, but can be made to intersect in the projective completion of A, a projective plane P, by adding the same point at infinity to each of the lines. In fact, this point at infinity must be added to all of the lines in the parallel class of lines that contains these two lines. Different parallel classes of lines of A will receive different points at infinity. The collection of all the points at infinity form the line at infinity. This line at infinity lies in P but not in A. Lines of A which meet in A will get different ideal points since they can not be in the same parallel class, while lines of A which are parallel will get the same ideal point.
In hyperbolic geometry, an ideal point is also called an omega point. Given a line l and a point P not on l, right- and left-limiting parallels to l through P are said to meet l at omega points (this is an abuse of language since these lines do not meet in the geometry). In the Poincaré disk model and the Klein model of hyperbolic geometry, the omega points can be visualized since they lie on the boundary circle (which is not part of the model). Pasch's axiom and the exterior angle theorem still hold for an omega triangle, defined by two points in hyperbolic space and an omega point.[1]
Generalisations
This construction can be generalized to an arbitrary topological space. The space so obtained is called the one-point compactification or Alexandroff compactification of the original space. Thus the circle is the one-point compactification of the line, and the sphere is the one-point compactification of the plane.